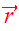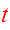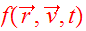Lecture 4 Collisionless Boltzmann Equation
Physics 141/241
Collisionless dynamics
A typical galaxy has
 stars but is only
stars but is only
 crossing times old, so the cumulative effects of encounters between stars are
not significant. This justifies the next step, which is to idealize a galaxy
as a continuous mass distribution. In this limit, each star moves in the
smooth gravitational field
crossing times old, so the cumulative effects of encounters between stars are
not significant. This justifies the next step, which is to idealize a galaxy
as a continuous mass distribution. In this limit, each star moves in the
smooth gravitational field
 of the galaxy. Thus instead of thinking about motion in a phase space of
of the galaxy. Thus instead of thinking about motion in a phase space of
 dimensions, we can think about motion in a phase space of just
dimensions, we can think about motion in a phase space of just
 dimensions. This is a very important simplification!
dimensions. This is a very important simplification!
Distribution function
Rather than keeping track of individual stars, a galaxy may be described by
the one-body distribution function; let

be the mass of stars in the phase-space volume
 at
(
at
(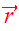 ,
, )
and time
)
and time
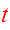 .
This provides a complete description if stars are uncorrelated, as assumed
above.
.
This provides a complete description if stars are uncorrelated, as assumed
above.
Collisionless Boltzmann equation
The motion of matter in phase space is governed by the phase space flow,

How does this affect the total amount of mass in the phase space volume
 ? The rate of change of the mass is just the inflow minus the outflow; that
is, the flow obeys a continuity equation in 6
dimensions:
? The rate of change of the mass is just the inflow minus the outflow; that
is, the flow obeys a continuity equation in 6
dimensions:
where the derivatives with respect to
 ,
and
,
and
 are understood to be partial derivatives. Using the expression for the
phase-flow yields the collisionless Boltzmann
equation:
are understood to be partial derivatives. Using the expression for the
phase-flow yields the collisionless Boltzmann
equation:
The collisionless Boltzmann equation or CBE describes the evolution of the
distribution function
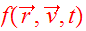 .
It serves as the fundamental equation of galactic dynamics.
.
It serves as the fundamental equation of galactic dynamics.
Fluid continuity equation
(See explanation with added class note here)
Gravity
The gravitational field
 is given self-consistently by Poisson's
equation,
is given self-consistently by Poisson's
equation,
Eqs. (4,5) may be viewed as a pair of coupled PDEs which together
completely describe the evolution of a galaxy.
Conservation of phase space density
Let
 be the orbit of a star. What is the rate of change of
be the orbit of a star. What is the rate of change of
 along the star's orbit? The answer is
zero,
along the star's orbit? The answer is
zero,
where the first equality is just the definition of the convective derivative
in phase-space, the second equality follows on substituting the phase-flow
(Eq. 2), and the last equality follows from the CBE (Eq. 4).
Thus, phase-space density is conserved along every orbit.
This fundamental and completely general result shows that the CBE has a much
greater level of symmetry than the N-body equations of motion; whereas the
latter conserves a fairly small set of parameters, the CBE conserves f(r,v,t)
along an infinite number of stellar orbits. We can take advantage of this
infinite array of conservation laws to obtain some important results even when
we can't explicitly solve the CBE.
Jeans Theorem
If the function
 is an integral which is conserved along any orbit:
is an integral which is conserved along any orbit:
 we can use the canonical equations to show that
we can use the canonical equations to show that
 is a steady state soultion of the CBE:
is a steady state soultion of the CBE:

Theorem: Any steady-state solution of the CBE
depends on the phase-space coordinates only through integrals of
motion in the galactic potential, and any function of the integrals yields a
steady-state solution of the CBE.
Proof: Suppose
 is a steady-state solution of CBE. Then
is a steady-state solution of CBE. Then
 is an integral, so that first part of theorem is true. Conversely, if
is an integral, so that first part of theorem is true. Conversely, if
 to
to
 are
are
 integrals, then
integrals, then

so that
 is an integral and a steady state solution of CBE.
is an integral and a steady state solution of CBE.
 stars but is only
stars but is only
 crossing times old, so the cumulative effects of encounters between stars are
not significant. This justifies the next step, which is to idealize a galaxy
as a continuous mass distribution. In this limit, each star moves in the
smooth gravitational field
crossing times old, so the cumulative effects of encounters between stars are
not significant. This justifies the next step, which is to idealize a galaxy
as a continuous mass distribution. In this limit, each star moves in the
smooth gravitational field
 of the galaxy. Thus instead of thinking about motion in a phase space of
of the galaxy. Thus instead of thinking about motion in a phase space of
 dimensions, we can think about motion in a phase space of just
dimensions, we can think about motion in a phase space of just
 dimensions. This is a very important simplification!
dimensions. This is a very important simplification!