Lecture 6 Virial Theorem and Jeans Theorem

Physics 141/241

Winter 2013

Collisionless Boltzmann Equation summary

The phase space density of mass, or Distribution Function (DF) of the N-body system was defined in Lecture 5 by considering the quantity

where 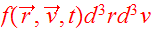designates the mass in the infinitesimal phase-space volume 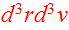around at time 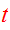. The DF 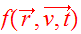satisfies the collisionless Boltzmann Equation (CBE),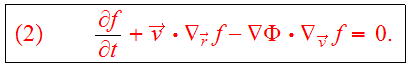

The collisionless Boltzmann equation describes the evolution of the distribution function and it serves as the fundamental equation of collisionless N-body dynamics. In components it is given by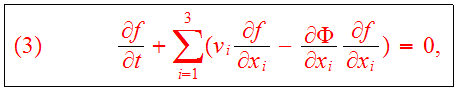

where the gravitational field is determined self-consistently by Poisson's equation,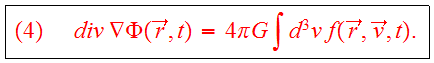

Eqs. (3,4) may be viewed as a pair of coupled PDEs which together completely describe the evolution of a galaxy.

Jeans Equations

Moments of the CBE contain important physics about time averages of the dynamical motion. Consider first the velocity moment of the CBE:

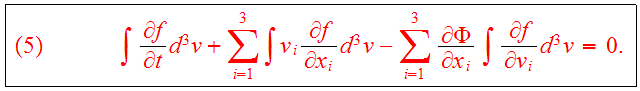
The following relation can be used for the mass density

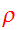
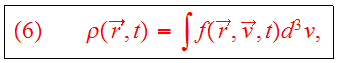
and the relation

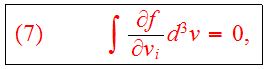
is valid, if 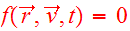for asymptotically large 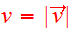. We introduce the average velocity,

and Eq. (5) becomes the continuity equation,

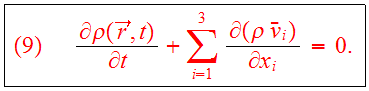
Consider now first moments in the velocity components:

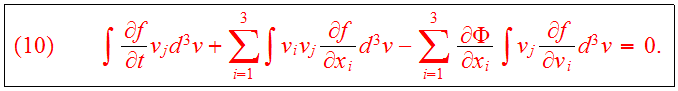
We use the identity

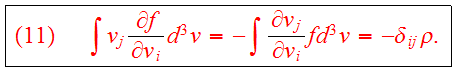
Define

which gives the Jeans equation for the first velocity moments:

Subtract 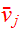times Eq.(9) from Eq.(13) :

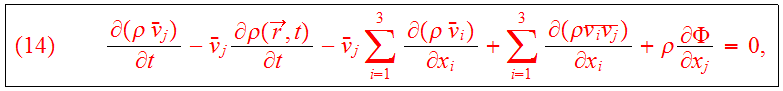
and define

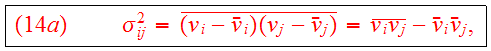
which describes the non-streaming motion locally. Eq.(14) becomes

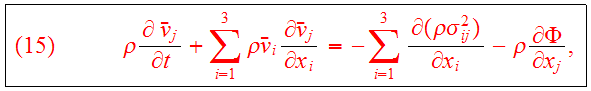
where 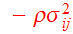is defined as the stress tensor. Eqs.(9,13,15) are known as the Jeans equations.

Virial Theorems

Multiply Eq.(13) by 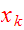and integrate over the spatial variables:

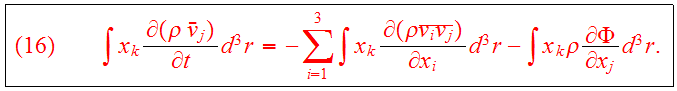
We introduce the potential energy tensor :

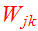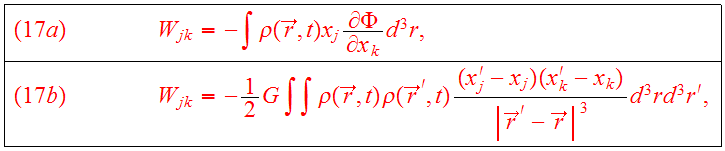
symmetric in the indices. The total gravitational potential energy is given by

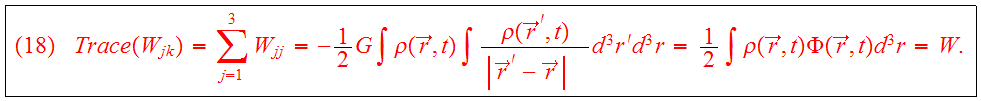
The following definition of the kinetic energy tensor 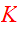will be used:

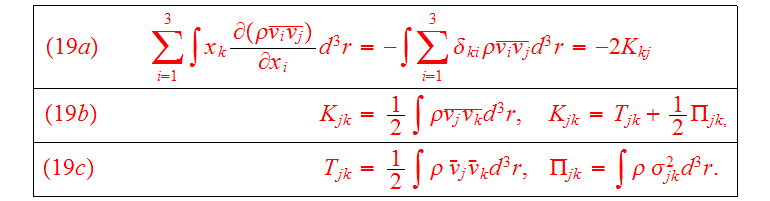
By averaging and 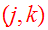in Eq.(16) and using the symmetry properties of the tensors, we get

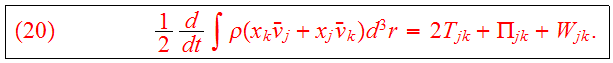
The moment of inertia tensor is defined as

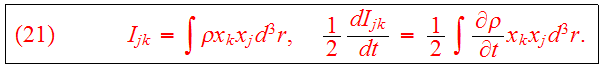
Using the continuity equation, we find

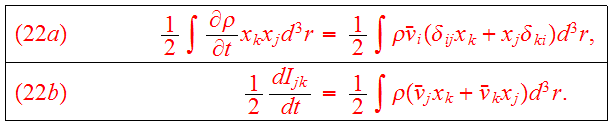
Combining Eqs.(20,22b) we obtain the tensor virial theorem:

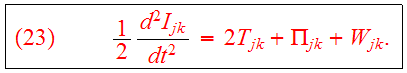
Since

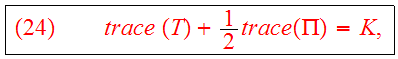
in steady state, , we get the scalar virial theorem:

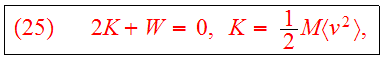
where M is the total mass of the system,

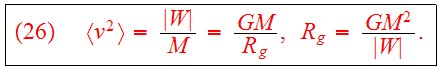
For the total energy, we find

and if stars are at rest at infinity; binding energy.

Jeans Theorem

If the function 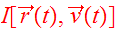is an integral which is conserved along any orbit: 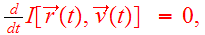we can use the canonical equations to show that is a steady state soultion of the CBE:

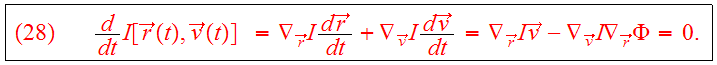
Theorem: Any steady-state solution of the CBE depends on the phase-space coordinates only through integrals of motion in the galactic potential, and any function of the integrals yields a steady-state solution of the CBE.

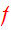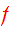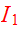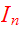Proof: Suppose is a steady-state solution of CBE. Then is an integral, so that first part of theorem is true. Conversely, if to are 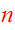integrals, then

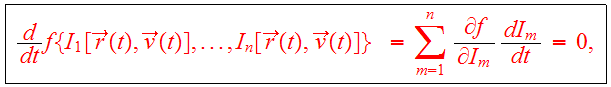
so that 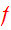is an integral and a steady state solution of CBE.