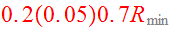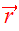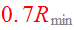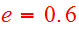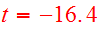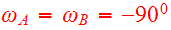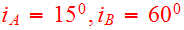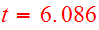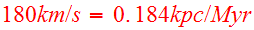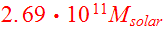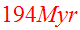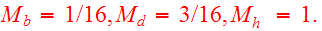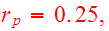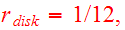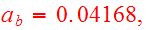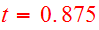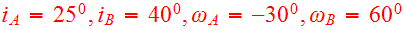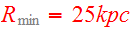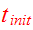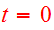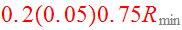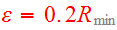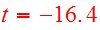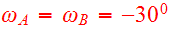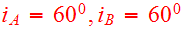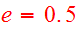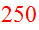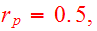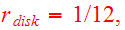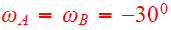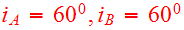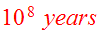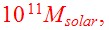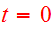Midterm and Final Team Projects
Physics 141/241
Winter 2012
All four teams work on the Midterm projects within the framework of
the Toomre&Toomre model of the restricted
three-body problem. The final projects are the best full simulations of the
teams using the bulge-disk-halo Dubinski model for their galaxy encounter
projects.
Previous Midterm project reports:
Mice
Antennae
Andromeda
Cartwheel
Midterm projects will be presented on March
14.
Final projects will be presented on March 23
between 2:00 pm - 5:00 pm.
The Mice Project (NGC 4676)
141 Team:Chu,Dang,Kelly,Singh
For convenience, Toomre&Toomre chose the time unit to be
 ,
the pericenter distance
,
the pericenter distance
 and the heavier mass in each encounter,
and the heavier mass in each encounter,
 ,
chosen as the mass unit. The collision orbits (elliptic, or parabolic) are
identified by choosing (1)
,
chosen as the mass unit. The collision orbits (elliptic, or parabolic) are
identified by choosing (1)
 and (2) the initial separation
and (2) the initial separation
 ,
or the equivalent time
,
or the equivalent time
 ,
with
,
with
 chosen at pericenter. Initial velocities are dependent on the masses of the
galaxies. Disk orientations and other input parameters are determined from the
reference material of the projects as requested in the project descriptions.
For the Midterm project Toomre&Toomre disk galaxy models
are prepared with test particles to run the restricted 3-body integrator. In
the Final project realistic Galaxies are crafted at the origin of the
coordinate system using the code of Konrad Kuijken and John Dubinski to
generate disk-bulge-halo galaxies. The code is discussed in the paper by
Kuijken&Dubinski and
the tar file of the code is packaged
galactics.tar.gz.
chosen at pericenter. Initial velocities are dependent on the masses of the
galaxies. Disk orientations and other input parameters are determined from the
reference material of the projects as requested in the project descriptions.
For the Midterm project Toomre&Toomre disk galaxy models
are prepared with test particles to run the restricted 3-body integrator. In
the Final project realistic Galaxies are crafted at the origin of the
coordinate system using the code of Konrad Kuijken and John Dubinski to
generate disk-bulge-halo galaxies. The code is discussed in the paper by
Kuijken&Dubinski and
the tar file of the code is packaged
galactics.tar.gz.
Midterm: Mice Project
Figure 22 on page 35 in Toomre&Toomre
summarizes the initial setup of their most successive Mice
encounter. Reproduce their result of Fig.22 using 297 disk particles in each
disk as described on page 20. They fill 11 concentric rings of radii
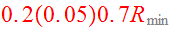 .
Increase the filling of the rings by increments of three test particles and
starting with
.
Increase the filling of the rings by increments of three test particles and
starting with
 particles on the innermost ring. The outermost ring has
particles on the innermost ring. The outermost ring has
 particles. Run your restricted 3-body code where the test particles are
tracking the two elliptic orbits of the core galaxies. The test particles are
interacting with the cores only. Work in the center-of-mass coordinate system
where the relative coordinate vector
particles. Run your restricted 3-body code where the test particles are
tracking the two elliptic orbits of the core galaxies. The test particles are
interacting with the cores only. Work in the center-of-mass coordinate system
where the relative coordinate vector
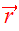 traces the elliptic Kepler orbit. For the elliptic orbits, use the appropriate
parametrization as it was outlined in Lecture 5:
traces the elliptic Kepler orbit. For the elliptic orbits, use the appropriate
parametrization as it was outlined in Lecture 5:

The origin of the CM coordinate system cn be chosen to coincide with the Sun
location of the figure. Two equal disks of radius
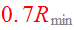 experience an elliptic encounter with
experience an elliptic encounter with
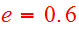 ,
having begun flat and circular at the time
,
having begun flat and circular at the time
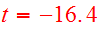 of the last apocenter. As viewed from either disk, the adopted node to peri
angles
of the last apocenter. As viewed from either disk, the adopted node to peri
angles
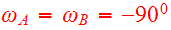 with inclinations
with inclinations
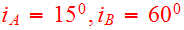 .
The angles are discussed in Fig. 6a,b (see also
Galaxy Rotations note and
collision orbit note). The resulting
composite object is shown at
.
The angles are discussed in Fig. 6a,b (see also
Galaxy Rotations note and
collision orbit note). The resulting
composite object is shown at
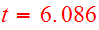 in Fig. 22.
in Fig. 22.
(1) Compare Toomre&Toomre to your simulation.
(2) Animate and make an Mpeg movie.
(3) Give a simple explanation of the tidal tails and explain
whether the tidal tails are in the plane of the rotating disks, or the
collision plane, or neither.
(4) Write a project report and prepare a 20 minutes
presentation.
Final: Project Mice
Barnes in his paper argued
that a realistic full simulation of the encounter using realistic
bulge-disk-halo galaxy model calls for parabolic encounter. He gave arguments
that the bulge-disk-halo galaxy structure requires to replace the elliptic
encounter of Toomre&Toomre with parabolic encounter. For the initial
condition, consider to separate galaxies on parabolic collision course. Galaxy
A and galaxy B do not overlap initially, and the center of masses of the
individual galaxies would continue on a parabolic orbit, if the interactions
of the stars would not change the picture when the galaxies begin to overlap.

First, we would like to set up the appropriate initial condition for the
collision as depicted in the figure above. Notes on the setup are given in
collision orbit note. Notes on the
disk angles are given in Galaxy Rotations
note. Barnes chose in the paper the length unit to be
 ,
the velocity unit as
,
the velocity unit as
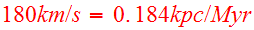 ,
and the mass unit as
,
and the mass unit as
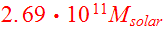 .
One time unit then works out to be
.
One time unit then works out to be
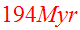 .
Barnes chose for the galaxy components:
.
Barnes chose for the galaxy components:
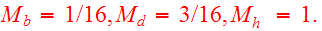 Parabolic orbit was chosen with
Parabolic orbit was chosen with
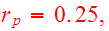
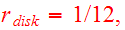
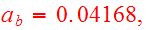

 .
The viewing time of the encounter is
.
The viewing time of the encounter is
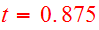 after pericenter. The disk angles are
after pericenter. The disk angles are
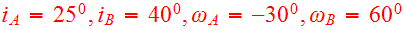 .
.
(1) Use the Galactics package to fabricate the initial
galaxies. Choose your resolution for the project.
(2) Run Gyrfalcon to reproduce the
results of Barnes in the article.
(3) Animate and make Mpeg movies of the project.
(4) Give again simple explanation of the consistency of tidal
tails with Toomre&Toomre and explain again whether the tidal tails are in
the plane of the rotating disks, or the collision plane, or neither.
(5) Write a project report and prepare a 20 minutes
presentation.
The Antennae Project (NGC 4038/9)
141 Team:Chang,Keldgord,Lin,Sacca,Spacek
For convenience, Toomre&Toomre chose the time unit to be
 ,
the pericenter distance
,
the pericenter distance
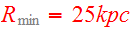 and the heavier mass in each encounter,
and the heavier mass in each encounter,
 chosen as the unit mass. The collision orbits (elliptic, or parabolic) are
identified by choosing (1)
chosen as the unit mass. The collision orbits (elliptic, or parabolic) are
identified by choosing (1)
 and (2) the initial separation
and (2) the initial separation
 ,
or the equivalent time
,
or the equivalent time
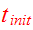 ,
with
,
with
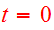 chosen at pericenter. Initial velocities are dependent on the masses of the
galaxies. Disk orientations and other input parameters are determined from the
reference material of the projects as requested in the project descriptions.
For the Midterm project Toomre&Toomre disk galaxy models
are prepared with test particles to run the restricted 3-body integrator. In
the Final project realistic Galaxies are crafted at the origin of the
coordinate system using the code of Konrad Kuijken and John Dubinski to
generate disk-bulge-halo galaxies. The code is discussed in the paper by
Kuijken&Dubinski and
the tar file of the code is packaged
Galactics.tar.gz.
chosen at pericenter. Initial velocities are dependent on the masses of the
galaxies. Disk orientations and other input parameters are determined from the
reference material of the projects as requested in the project descriptions.
For the Midterm project Toomre&Toomre disk galaxy models
are prepared with test particles to run the restricted 3-body integrator. In
the Final project realistic Galaxies are crafted at the origin of the
coordinate system using the code of Konrad Kuijken and John Dubinski to
generate disk-bulge-halo galaxies. The code is discussed in the paper by
Kuijken&Dubinski and
the tar file of the code is packaged
Galactics.tar.gz.
Midterm: Antennae Project
Figure 23 on page 37 in Toomre&Toomre
summarizes the initial setup of their symmetric Antennae
encounter. Reproduce their result of Fig.23 using 345 disk particles in each
disk as described on page 20. They fill 12 concentric rings of radii
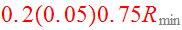 .
Increase the filling of the rings by increments of three test particles added
to the next ring and starting with
.
Increase the filling of the rings by increments of three test particles added
to the next ring and starting with
 particles on the innermost ring. The outermost ring has
particles on the innermost ring. The outermost ring has
 particles. Run your restricted 3-body code where the test particles are
tracking the two elliptic orbits of the core galaxies with
particles. Run your restricted 3-body code where the test particles are
tracking the two elliptic orbits of the core galaxies with
 .
The test particles are interacting with the cores only and the interaction is
softened by
.
The test particles are interacting with the cores only and the interaction is
softened by
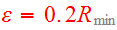 at the closest range to mimic the distributed mass of the real object. Work in
the center-of-mass coordinate system where the relative coordinate vector
at the closest range to mimic the distributed mass of the real object. Work in
the center-of-mass coordinate system where the relative coordinate vector
 traces the elliptic Kepler orbit. For the elliptic orbits, use the appropriate
parametrization as it was outlined in Lecture 5:
traces the elliptic Kepler orbit. For the elliptic orbits, use the appropriate
parametrization as it was outlined in Lecture 5:
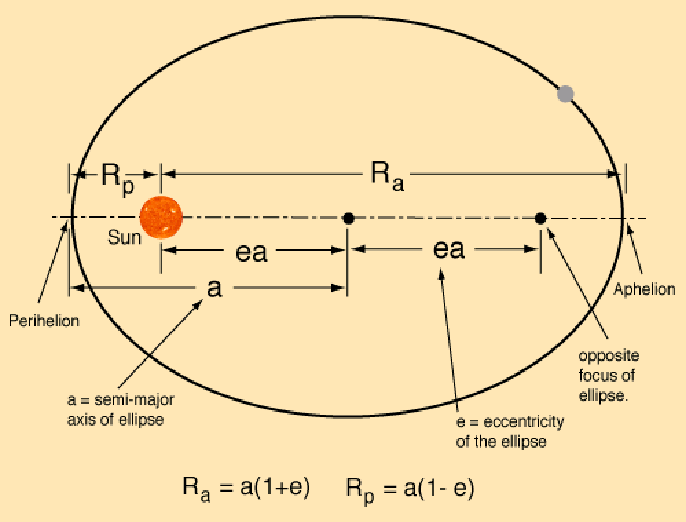
The origin of the CM coordinate system can be chosen to coincide with the Sun
location of the figure. Two equal disks of radius
 experience an elliptic encounter, having begun flat and circular at the time
experience an elliptic encounter, having begun flat and circular at the time
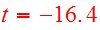 of the last apocenter. As viewed from either disk, the adopted node to peri
angles
of the last apocenter. As viewed from either disk, the adopted node to peri
angles
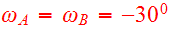 with inclinations
with inclinations
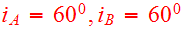 .
The angles are discussed in Fig. 6a,b (see also
Galaxy Rotations note and
collision orbit note). The viewing
time of the resulting composite object is
.
The angles are discussed in Fig. 6a,b (see also
Galaxy Rotations note and
collision orbit note). The viewing
time of the resulting composite object is
 in Fig. 23.
in Fig. 23.
(1) Compare Toomre&Toomre to your simulation.
(2) Animate and make an Mpeg movie.
(3) Give a simple explanation of the tidal tails and explain
whether the tidal tails are in the plane of the rotating disks, or the
collision plane, or neither.
(4) Write a project report and prepare a 20 minutes
presentation.
Final: Antennae Project
Barnes in his paper on the
Antennae designed a realistic full simulation of the encounter
using realistic bulge-disk-halo galaxy model with elliptic encounter. For the
initial condition, consider to separate galaxies on elliptic collision course
with
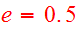 .
Galaxy A and galaxy B do not overlap initially, and the center of masses of
the individual galaxies would continue on an elliptic orbit, if the
interactions of the stars would not change the picture when the galaxies begin
to overlap.
.
Galaxy A and galaxy B do not overlap initially, and the center of masses of
the individual galaxies would continue on an elliptic orbit, if the
interactions of the stars would not change the picture when the galaxies begin
to overlap.

First, we would like to set up the appropriate initial condition for the
collision as depicted in the figure above, but the parbolic orbits replaced by
elliptic ones. Notes on the setup for parbolic orbits are given in
collision orbit note and have to be
replaced by the properties of elliptic
orbits. Notes on the disk angles are given in
Galaxy Rotations note. Barnes chose
in the paper the length unit to be
 ,
and the mass unit as
,
and the mass unit as
 .
One time unit is
.
One time unit is
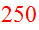
 .
Barnes chose for the galaxy components:
.
Barnes chose for the galaxy components:
 with a total mass
with a total mass
 Elliptic orbits were chosen and started with
Elliptic orbits were chosen and started with
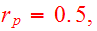
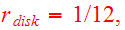 node to peri angles
node to peri angles
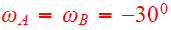 with inclinations
with inclinations
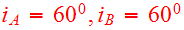 and time
and time
 to epicenter to produce a slow and symmetrically prograde encounter with the
two disks inclined so as to sling tidal tails high above the orbital plane
where they will eventually be seen in projection as crossing each other. The
viewing time of the encounter is close to the nex apocenter.
to epicenter to produce a slow and symmetrically prograde encounter with the
two disks inclined so as to sling tidal tails high above the orbital plane
where they will eventually be seen in projection as crossing each other. The
viewing time of the encounter is close to the nex apocenter.
(1) Use the Galactics package to fabricate the initial
galaxies. Choose your resolution for the project.
(2) Run Gyrfalcon to reproduce the
results of Barnes in the article.
(3) Animate and make Mpeg movies of the project.
(4) Give again simple explanation of the consistency of tidal
tails with Toomre&Toomre and explain again whether the tidal tails are in
the plane of the rotating disks, or the collision plane, or neither.
(5) Write a project report and prepare a 20 minutes
presentation.
Andromeda Project
241 Team:Hverven,Kokate,Thon,Ye
For convenience, Toomre&Toomre chose the time unit to be
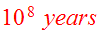 ,
the pericenter distance
,
the pericenter distance
 and the heavier mass in each encounter,
and the heavier mass in each encounter,
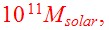 chosen as the unit mass. The collision orbits (elliptic, or parabolic) are
identified by choosing (1)
chosen as the unit mass. The collision orbits (elliptic, or parabolic) are
identified by choosing (1)
 and (2) the initial separation
and (2) the initial separation
 ,
or the equivalent time
,
or the equivalent time
 ,
with
,
with
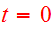 chosen at pericenter. Initial velocities are dependent on the masses of the
galaxies. Disk orientations and other input parameters are determined from the
reference material of the projects as requested in the project descriptions.
For the Midterm project Toomre&Toomre disk galaxy models
are prepared with test particles to run the restricted 3-body integrator. In
the Final project realistic Galaxies are crafted at the origin of the
coordinate system using the code of Konrad Kuijken and John Dubinski to
generate disk-bulge-halo galaxies. The code is discussed in the paper by
Kuijken&Dubinski and
the tar file of the code is packaged
Galactics.tar.gz.
chosen at pericenter. Initial velocities are dependent on the masses of the
galaxies. Disk orientations and other input parameters are determined from the
reference material of the projects as requested in the project descriptions.
For the Midterm project Toomre&Toomre disk galaxy models
are prepared with test particles to run the restricted 3-body integrator. In
the Final project realistic Galaxies are crafted at the origin of the
coordinate system using the code of Konrad Kuijken and John Dubinski to
generate disk-bulge-halo galaxies. The code is discussed in the paper by
Kuijken&Dubinski and
the tar file of the code is packaged
Galactics.tar.gz.
Midterm: Andromeda Project
Use Section 4.4 of the paper by Dubinski et
al. to set up the run conditions for the collision of the Milky
Way with Andromeda using a Toomre&Toomre model in the spirit of the Mice
and Antennae projects. Run your restricted 3-body code where the test
particles are tracking the two elliptic orbits of the core galaxies with your
choice of
 .
The test particles are interacting with the cores only. Work in the
center-of-mass coordinate system where the relative coordinate vector
.
The test particles are interacting with the cores only. Work in the
center-of-mass coordinate system where the relative coordinate vector
 traces the elliptic Kepler orbit. For the elliptic orbits, use the appropriate
parametrization as it was outlined in Lecture 5:
traces the elliptic Kepler orbit. For the elliptic orbits, use the appropriate
parametrization as it was outlined in Lecture 5:

The origin of the CM coordinate system can be chosen to coincide with the Sun
location of the figure.
(1) Obtain Toomre&Toomre models mimicking the mergers of
Fig. 13 in Dubinski et al.
(2) Animate and make Mpeg movies of your mergers.
(3) Give a simple explanation of the tidal tails and explain
whether the tidal tails are in the plane of the rotating disks, or the
collision plane, or neither.
(4) Write a project report and prepare a 20 minutes
presentation.
Final: Andromeda Project
Dubinski et al. designed a
realistic full simulation of the encounter using realistic bulge-disk-halo
galaxy model with elliptic encounter. For the initial condition, consider to
separate galaxies on elliptic collision course with your choice of
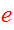 .
Galaxy A and galaxy B do not overlap initially, and the center of masses of
the individual galaxies would continue on an elliptic orbit, if the
interactions of the stars would not change the picture when the galaxies begin
to overlap.
.
Galaxy A and galaxy B do not overlap initially, and the center of masses of
the individual galaxies would continue on an elliptic orbit, if the
interactions of the stars would not change the picture when the galaxies begin
to overlap.
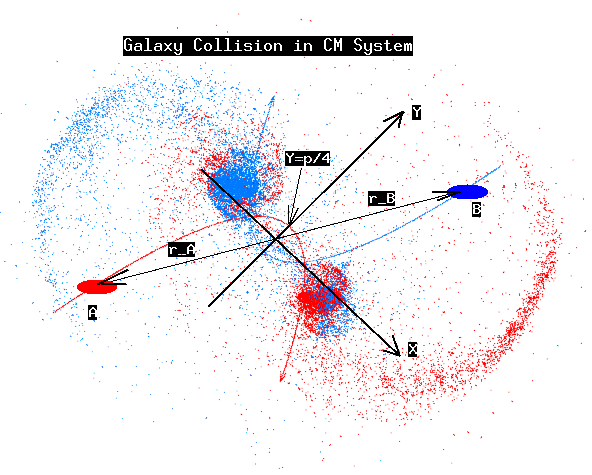
First, we would like to set up the appropriate initial condition for the
collision as depicted in the figure above, but the parbolic orbits replaced by
elliptic ones. Notes on the setup for parbolic orbits are given in
collision orbit note and have to be
replaced by the properties of elliptic
orbits. Notes on the disk angles are given in
Galaxy Rotations note. Set up your
initial conditions for the merger runs close to the models discussed in
Dubinski et al.
in Section 4.4.
(1) Use the Galactics package to fabricate the initial
galaxies. Choose your resolution for the project.
(2) Run Gyrfalcon to get close to
the results of Dubinski et al. as reported in Fig. 13 in the article.
(3) Animate and make Mpeg movies of the project.
(4) Give again simple explanation of the consistency of tidal
tails with Toomre&Toomre and explain again whether the tidal tails are in
the plane of the rotating disks, or the collision plane, or neither.
(5) Write a project report and prepare a 20 minutes
presentation.
Cartwheel Project
241 Team: Chen,Dai,Holladay,Yue
Midterm: Cartwheel
In the spirit of the Toomre&Toomre modeling of the Mice, Antennae, and
Milky Way mergers, study the paper by
Lynds&Toomre to set up and reproduce their model.
(1) Obtain Lynds&Toomre models mimicking the mergers of
Figs. 5 and 6 in the paper.
(2) Animate and make Mpeg movies of your mergers.
(3) Give a simple explanation of the Cartwheel.
(4) Write a project report and prepare a 20 minutes
presentation.
Final: Cartwheel
In the spirit of realistic modeling of galaxy mergers, like the Mice,
Antennae, and Milky Way mergers, study the
paper by Athanassoula et
al. to set up and reproduce their model of the Cartwheel using
bulge-disk-halo galaxies.
(1) Use the Galactics package to fabricate the initial
galaxies. Choose your resolution for the project.
(2) Run Gyrfalcon to get close to
the results of Athanassoula et al. as reported in their paper. Consider also the Aarseth code, if
it suits better the project, in case of demand on accuracy.
(3) Animate and make Mpeg movies of the project.
(4) Give again simple explanation of how the Cartwheel merger
happened.
(5) Write a project report and prepare a 20 minutes
presentation.
 ,
the pericenter distance
,
the pericenter distance
 and the heavier mass in each encounter,
and the heavier mass in each encounter,
 ,
chosen as the mass unit. The collision orbits (elliptic, or parabolic) are
identified by choosing (1)
,
chosen as the mass unit. The collision orbits (elliptic, or parabolic) are
identified by choosing (1)
 and (2) the initial separation
and (2) the initial separation
 ,
or the equivalent time
,
or the equivalent time
 ,
with
,
with
 chosen at pericenter. Initial velocities are dependent on the masses of the
galaxies. Disk orientations and other input parameters are determined from the
reference material of the projects as requested in the project descriptions.
For the Midterm project Toomre&Toomre disk galaxy models
are prepared with test particles to run the restricted 3-body integrator. In
the Final project realistic Galaxies are crafted at the origin of the
coordinate system using the code of Konrad Kuijken and John Dubinski to
generate disk-bulge-halo galaxies. The code is discussed in the paper by
Kuijken&Dubinski and
the tar file of the code is packaged
galactics.tar.gz.
chosen at pericenter. Initial velocities are dependent on the masses of the
galaxies. Disk orientations and other input parameters are determined from the
reference material of the projects as requested in the project descriptions.
For the Midterm project Toomre&Toomre disk galaxy models
are prepared with test particles to run the restricted 3-body integrator. In
the Final project realistic Galaxies are crafted at the origin of the
coordinate system using the code of Konrad Kuijken and John Dubinski to
generate disk-bulge-halo galaxies. The code is discussed in the paper by
Kuijken&Dubinski and
the tar file of the code is packaged
galactics.tar.gz.