PHYSICS 142/242

Spring 2010

Lecture 15:

Fluid Mechanics and Baseball Physics (PDF Document)

---

Flow around balls, circles, cylinders, etc.

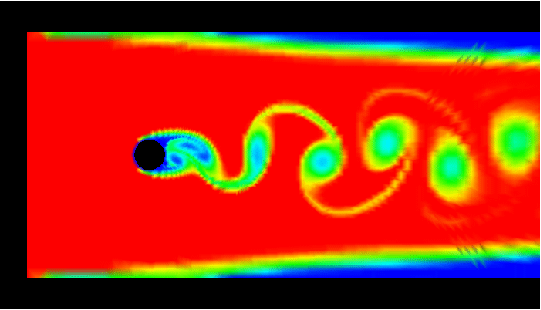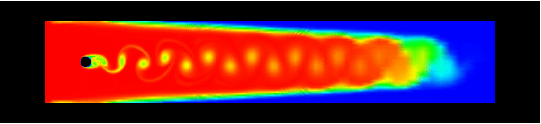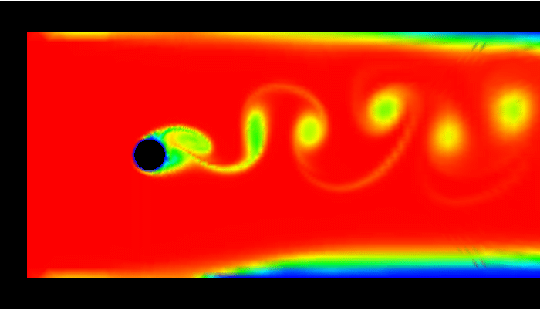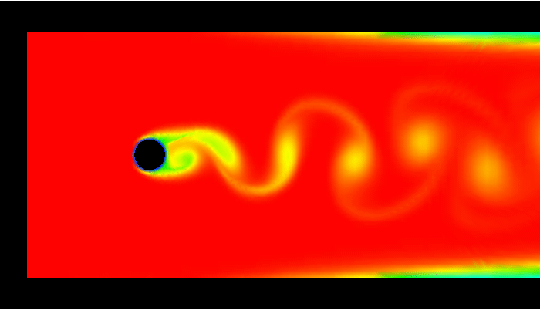
The following examples show flows through channels, around a set of obstacles, as for instance circles and balls.

Right after the obstacle(s), the flow separates and produces complex flow patterns, oscillating in space and time. In many applications, the corresponding drag and lift forces acting on the obstacle(s) are of major interest, and a difficult numerical job to do! The complexity of the problem depends on the:

• inflow speed
• rotational speed of the obstacles
• viscosity
• size and distance of the obstacles, w.r.t. to the channel walls and to each other

Flow around a (volley)ball in a channel at medium Reynolds number. The aim of this study by students is to demonstrate the influence of the rotation of a volleyball. The values to be controlled were the drag and lift forces which mainly determine the length and speed of a service, and the difficulty of return.

The following diagrams show the resulting drag and lift coefficients in time. While the speed of the (volley)ball was assumed to be 1.5, the rotational speeds were 0 (no rotation!), 0.1, 1 and 5. While the first three configurations (rotation speed less or almost equal the speed of the ball) are very similar, the fourth leads to non-comparable results.

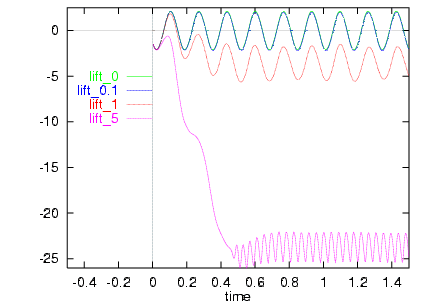
As can be seen, the additional rotation leads to more negative lift coefficients (that means the ball will "break sooner"), and the drag forces increase!For a comparison, see the corresponding results for the higher Reynolds number configuration. It might be interesting to make the same tests for a even more realistic Reynolds number, without a channel configuration, and to examine the effect of additional 3D effets.

Description of the flow problem

• length of channel: 2.2, height 0.4, diameter of circle: 0.05
• inflow b.c.'s: parabolic with (maximum) velocity 1.5 at the left edge
• outflow b.c.'s: natural "do nothing" b.c.'s
• circle b.c.'s: rotational tangential speed of size 0 (no slip), 0.1, 1 and 5
• other b.c.'s: zero velocity at fixed walls
• initial condition at t=0: starting from fully developed
• viscosity parameter: 1/nu=50,000

Description of the spatial discretization

• coarse mesh (=level 1): 130 cells, 156 vertices, 702 d.o.f.`s
  

  
  
  

• uniform refinements with exact boundary adaption
• visualization on level 4: 8,320 cells, 8,528 vertices, 42,016 d.o.f.`s
• computing mesh on level 7: 532,480 cells, 534,144 vertices, 2,665,728 d.o.f.`s
• nonconforming nonparametric rotated bilinear fem's (meanvalue version), UPW

Description of the temporal discretization

• equidistant time stepping for computation with k=0.00111112
• equidistant time stepping for visualization with k=0.01 (= 1 frame)
• Total time T=1.5 corresponds to 1,350 time steps
• fractional step theta scheme

• Distribution of temperature/concentration via Boussinesq model
  
  

  Visualization via tracing of concentration, starts from the inlet. Each row contains the videos for a zoomed representation with two different color maps (all about 1.1 MB, resp., 1.5 MB), and the video for the complete domain (about 0.9 MB each). The first row is for rotational speed 0 (no rotation), then followed by 0.1 (second), 1 (third) and finally for rotational speed 5 (fourth row).
  

  
  

  
  

  
  

  
  
  

  ---